* Logistic Classification
- 주어진 두개의 값 중 하나의 값을 예측 하는 것
- Binary Classification
ex) 스팸메세지인지 햄인지 구분하는 것, 페이스북 피드 show and hide
* (예시) 공부 시간에 따른 Pass(1) and fail(0)
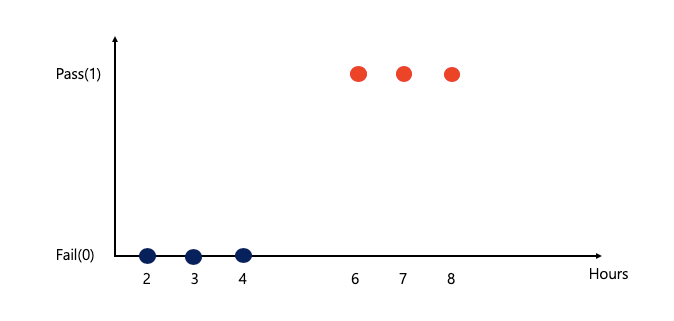
- Linear Regression 으로 표현 불가능한 이유
1) training set이 너무 큰 값으로 예측하면 예측점(0.5)이 변하기 때문에 예측이 틀림 (기준 값(0.5) 이상은 pass)
: 6시간, 7시간 공부한 사람은 Pass지만 Fail로 에측됨
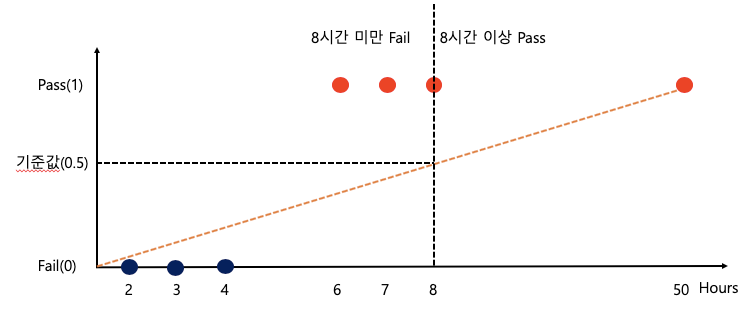
2) 너무 큰 training set의 경우 Hypothesis 값과 차이가 너무 많이남
H(x) = 2 * X 일 때(W는 2일 때), X가 50인 사람은 H(x)값은 100 이지만 실제 Pass(1)로 계산 되므로 값의 차이가 많이 남
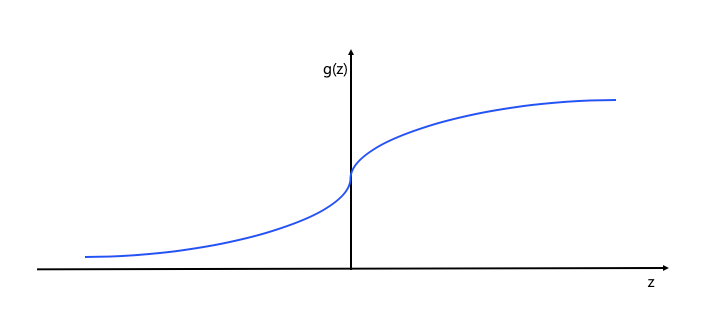
* Logistic Hypothesis는 Sigmoid 함수를 사용
- z가 커지면 1에 가까워 짐
- z가 작아지면 0에 가까워 짐
- Weight와 X의 곱을 z 로 정의 하고, sigmoid 함수를 적용

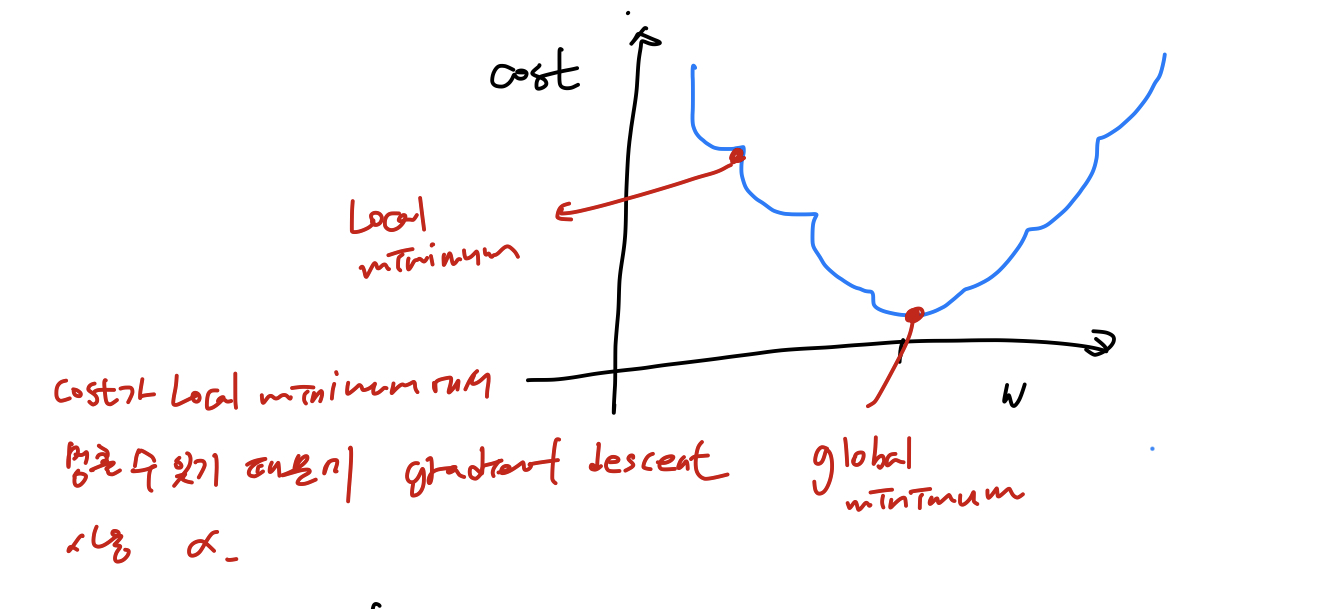
* Cost Function - Gradient Descent
- 기존 cost function을 사용하면 Gradient Descent 를 사용 할 수 없음
- Logical minimum을 cost가 가장 작은 값으로 예측 할 수 있기 때문
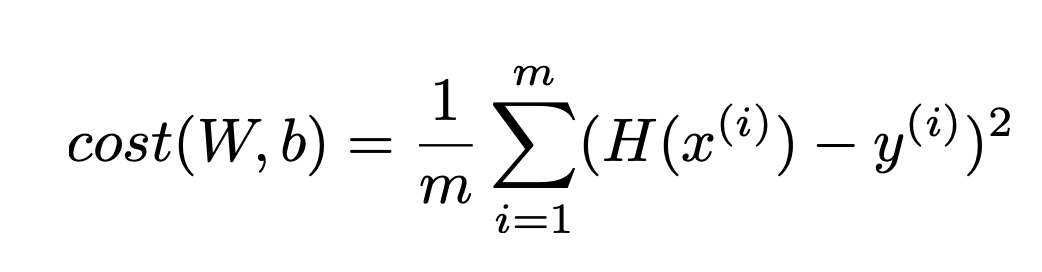
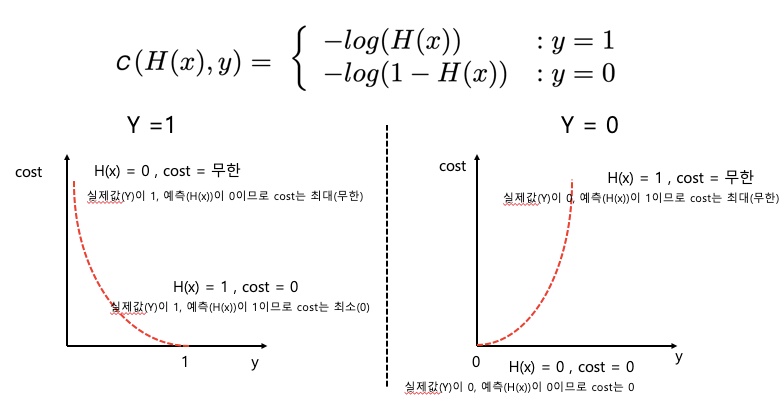
* Logistic classficiation의 Cost 함수
- 수식으로 표현
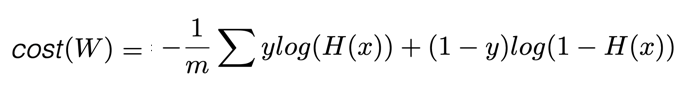
* Gradient Descent
W := W - 미분(cost(W))
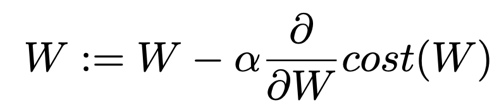
* 실습
import tensorflow as tf
x_data = [[1,2],[2,3],[3,1],[4,3],[5,3],[6,2]]
y_data = [[0],[0],[0],[1],[1],[1]]
X = tf.placeholder(tf.float32, shape=[None,2])
Y = tf.placeholder(tf.float32, shape=[None,1])
W = tf.Variable(tf.random_normal([2,1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
#tf.matmul(X,W) + b => WX
hypothesis = tf.sigmoid(tf.matmul(X,W) + b)
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y)*tf.log(1 - hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)
# hypothesis가 0.5 보다 크면 1
# hypothesis가 0.5보다 같거나 작으면 0
# dtype=flaot32로 케스팅 하면 true는 1, false는 0 이 됨
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted,Y), dtype=tf.float32))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(10001):
cost_val, _ = sess.run([cost,train], feed_dict={X: x_data, Y:y_data})
if step % 2000 == 0:
print(step, cost_val)
h, c, a = sess.run([hypothesis, predicted, accuracy],
feed_dict={X:x_data,Y:y_data})
print("\nHyopthesis: ",h, "\nCorrect (Y) : ", c, "\n Accuracy: ",a)
출처: 모두를 위한 딥러닝 유튜브
'개발자 > 모두를 위한 딥러닝' 카테고리의 다른 글
| 07. Application & Tips (0) | 2020.02.16 |
|---|---|
| 06.Multinomial classification - Softmax Classification (0) | 2020.02.14 |
| 04.Multi-variable linear regression (0) | 2020.02.13 |
| 03. How to minimize cost - Gradient Descent Algorithm (0) | 2020.02.12 |
| 02. Linear Regression (0) | 2020.02.12 |



